Monday, May 18, 2015
Sacred math, secular math
Started thinking about 'home ec' versus 'ec'. The name 'home ec' was an attempt by the humble Useful Trades to slide upward into colleges where the arrogant and imperial Useless Arts dominated. Industrial training for the farmer and the grocer and the housewife tried to wear the velvet cloaks of Holy Theory. It didn't hold up. The high priests of Sacred Uselessness eventually kicked out the Secular Useful Trades. Ideally the Secular Useful Trades shouldn't have humbly begged. Ideally they should have tortured and shot the Sacred Useless Arts and displayed their bloody heads on spikes.
This line of thought led to some questions.
= = = = =
Question #1: Is there a basic difference between Secular and Sacred math?
Answer: Yes.
High-theory math, cutting-edge math, is high-church math. It always serves a religion. A thousand years ago, high-church math served the needs of prayer and liturgy. Catholics developed astronomy and time-keeping to a high level to insure that Easter and other holy days were observed at exactly the right time. Muslims worked on geometry and trig to insure that prayers were pointing exactly at Mecca.
As the center of religion shifted, the center of scholarly math shifted as well, leading to a sudden reversal around 1800. Newton worked to serve a private mystical version of Christianity, and Laplace explicitly switched the focus to anti-theism, where it's been ever since.
Modern math scholars are always strongly religious in the modern sense. Their work specifically serves the evangelical advance of ferocious sadistic Dawkins/Darwin Gaia worship and murderous anti-theism. They are Dawkins jihadis.
Some pieces of scholarly math have escaped into non-priestly use, but they never make it all the way "down" into the secular masses. Calculus and algebra remain in the diaconate of engineers.
= = = = =
Secular math has not "advanced" into "new territory" because it doesn't feel the need. Secular math serves the merchant, the farmer, the carpenter, the cook, the housewife. Secular math includes the four basic functions and proportions and angles. (Not really trig as such; usually a written or internalized 'lookup table' for sin and cos.)
Our secular calculating devices, from written numerals to abacuses to computers, have always added and subtracted easily. Mult and div are tricky, and proportions simply don't work on these devices. We've developed other devices for proportions, often direct analog computers based on lever arms or gears. The slide rule is the ultimate proportioner, but it requires considerable skill and it doesn't SHOW the proportions nearly as well as an analog mechanism.
What's missing here? (If you've been reading this blog regularly, you know exactly what I'm going to say next.)
TANH! Everything we do in the real secular world, including everything our own bodies do with measurements, is loggish. Sometimes the result is Tanh, sometimes a two-ended Tanh with constraints at both ends. I call it a tuning curve because it's what you get from a bandpass filter.
The basic formula would be like
y = tanh(x) * tanh(c-x) where c defines the width of the hump.
Fussy but important: This shape looks like the bell curve or normal distribution, but the math for the bell doesn't conform to reality as well as the two-sided tanh. Real situations are more like a mesa than a peak, more like a mole than a zit. There's always a flat spot in the middle; sometimes the flat spot covers nearly all of the available range and sometimes the flat spot is zeroed out to provide a peak. The bell math always gives you a peak point.
Polistra tries to show the difference. First the bell curve:
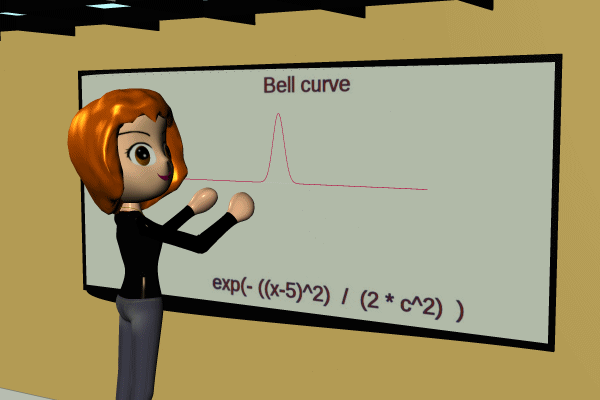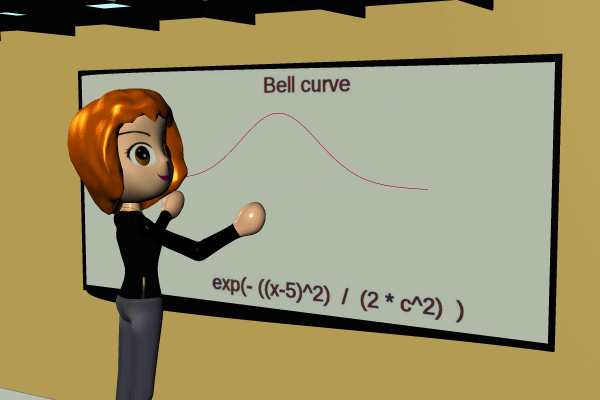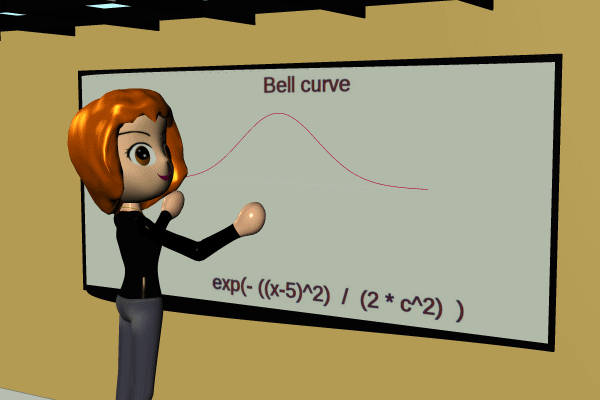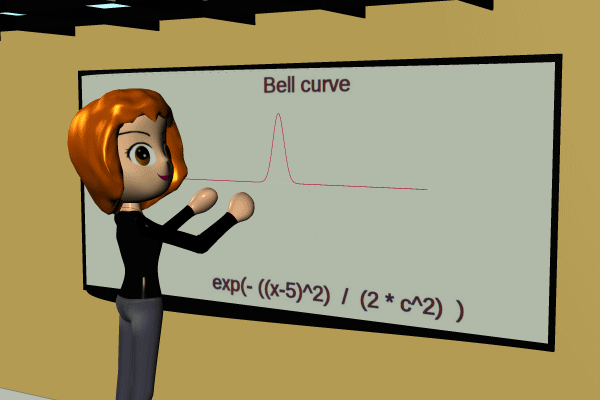 Now the tuning curve:
Now the tuning curve:
 I'm NOT saying that the bell should be replaced by tanh. I'm only showing the distinction dynamically because the tuning curve is unfamiliar. Bell works nicely for stat distributions; one-sided tanh works for most input-output situations (transfer functions) in life, and two-sided tanh it forms the life-patterns of critters and organizations.
The math for the tuning curve is complicated. Computers can handle it, but there should be a nicer way of calculating such a basic and necessary shape. Secular math ought to find a cleaner way of doing it and writing it, whether by an analog calculator or by a single button on a digital calculator.
Another piece of everyday secular math that is NOT handled by sacred math is 'bracketizing', a calculation that uses integers and continua in separate ways, boundaried by decisions, thresholds or containers. I discussed it in the grocery context here and here. Bracketizing also appears in tax forms. When Alleged Einstein called income tax the hardest math problem, he was speaking from a Sacred Math mindset. Calculations like this cannot be turned into a closed-form Sacred equation no matter how hard you try. If line 37 is greater than 3.2 times line 12a, multiply by 0.376; otherwise add 12 and divide by 5.021. A computer program can handle those mixes of decisions and operations, but ideally there should be a way to handle them in 'pure' Secular math.
= = = = =
Question #2: If everything in our life and senses runs logly, why did so much of secular math develop as pure linear addition and subtraction?
Answer: Because one important sense is NOT loggish.
Our senses of pressure and weight are linear. When I put one item, two items, three items, in your hand, the weight-measuring inputs to your brain are linear and even countable. A fast series of pulses from your muscle spindles.
What does that remind you of? Money. One shell, two shells, three shells. One coin, two coins, three coins. Money began as weight, and many monetary units still denote weights.
Because we weighed gold and silver, we became accustomed to treating money, and then transactions involving money, in linear form ... EVEN THOUGH the transactions and our judgments and feelings about the transactions are loggish.
Our sense of relative income is unquestionably log or percentage-based. Even economists have figured this out. As with decibels or lumens, our judgments are the log of the underlying quantity. "My neighbor is one step above me in income" = neighbor has 3 * my income. "If I could jump one step up in wealth I'd be satisfied" = If I had 3 * current wealth I'd be satisfied.
Actual prices of actual goods are also loggish. This is somewhat disguised by the piecewise linearity of a small part of any curve, but when you scale up you can see it. Two cans of soup = same price as one can + one can. Twenty cans of soup cost less than 20 * one can. A thousand cans cost MUCH less than 1000 * one can.
Because overhead is relatively constant, price is a loggish function of quantity.
= = = = =
Question #3: How would commerce and everyday life differ if we had a more loglike system of secular math?
Unanswered for now. As usual, I'm hoping to return to this. As usual, I probably won't.
Later partial answer or starting point.
= = = = =
Bonus:
I've supplied an attempted 'easy proportioner' or 'software slide rule' as mentioned above.
I'm NOT saying that the bell should be replaced by tanh. I'm only showing the distinction dynamically because the tuning curve is unfamiliar. Bell works nicely for stat distributions; one-sided tanh works for most input-output situations (transfer functions) in life, and two-sided tanh it forms the life-patterns of critters and organizations.
The math for the tuning curve is complicated. Computers can handle it, but there should be a nicer way of calculating such a basic and necessary shape. Secular math ought to find a cleaner way of doing it and writing it, whether by an analog calculator or by a single button on a digital calculator.
Another piece of everyday secular math that is NOT handled by sacred math is 'bracketizing', a calculation that uses integers and continua in separate ways, boundaried by decisions, thresholds or containers. I discussed it in the grocery context here and here. Bracketizing also appears in tax forms. When Alleged Einstein called income tax the hardest math problem, he was speaking from a Sacred Math mindset. Calculations like this cannot be turned into a closed-form Sacred equation no matter how hard you try. If line 37 is greater than 3.2 times line 12a, multiply by 0.376; otherwise add 12 and divide by 5.021. A computer program can handle those mixes of decisions and operations, but ideally there should be a way to handle them in 'pure' Secular math.
= = = = =
Question #2: If everything in our life and senses runs logly, why did so much of secular math develop as pure linear addition and subtraction?
Answer: Because one important sense is NOT loggish.
Our senses of pressure and weight are linear. When I put one item, two items, three items, in your hand, the weight-measuring inputs to your brain are linear and even countable. A fast series of pulses from your muscle spindles.
What does that remind you of? Money. One shell, two shells, three shells. One coin, two coins, three coins. Money began as weight, and many monetary units still denote weights.
Because we weighed gold and silver, we became accustomed to treating money, and then transactions involving money, in linear form ... EVEN THOUGH the transactions and our judgments and feelings about the transactions are loggish.
Our sense of relative income is unquestionably log or percentage-based. Even economists have figured this out. As with decibels or lumens, our judgments are the log of the underlying quantity. "My neighbor is one step above me in income" = neighbor has 3 * my income. "If I could jump one step up in wealth I'd be satisfied" = If I had 3 * current wealth I'd be satisfied.
Actual prices of actual goods are also loggish. This is somewhat disguised by the piecewise linearity of a small part of any curve, but when you scale up you can see it. Two cans of soup = same price as one can + one can. Twenty cans of soup cost less than 20 * one can. A thousand cans cost MUCH less than 1000 * one can.
Because overhead is relatively constant, price is a loggish function of quantity.
= = = = =
Question #3: How would commerce and everyday life differ if we had a more loglike system of secular math?
Unanswered for now. As usual, I'm hoping to return to this. As usual, I probably won't.
Later partial answer or starting point.
= = = = =
Bonus:
I've supplied an attempted 'easy proportioner' or 'software slide rule' as mentioned above.
 The proportioner is here. The ZIP contains a (hopefully) self-explanatory Python program. It has an Input side, a Ratio, and an Output side. When you fill in either the numerator or denominator on the Input side, the Ratio shows and the Output side changes appropriately. When you fill in numerator or denominator on the Output side, the Ratio doesn't change, but the other member on the Output side changes.
I've been wanting this little helper for a long time, especially to deal with Aspect Ratio in images. You may find other uses.
The proportioner is here. The ZIP contains a (hopefully) self-explanatory Python program. It has an Input side, a Ratio, and an Output side. When you fill in either the numerator or denominator on the Input side, the Ratio shows and the Output side changes appropriately. When you fill in numerator or denominator on the Output side, the Ratio doesn't change, but the other member on the Output side changes.
I've been wanting this little helper for a long time, especially to deal with Aspect Ratio in images. You may find other uses.
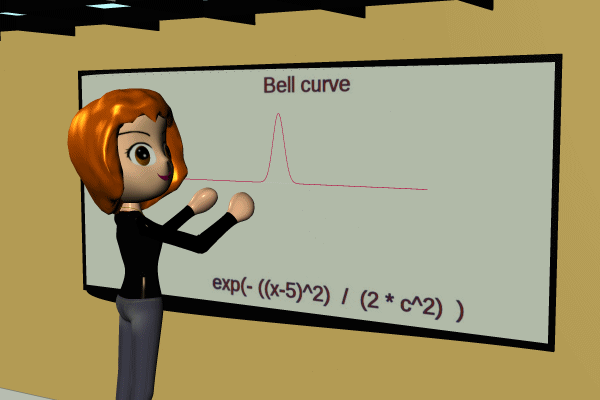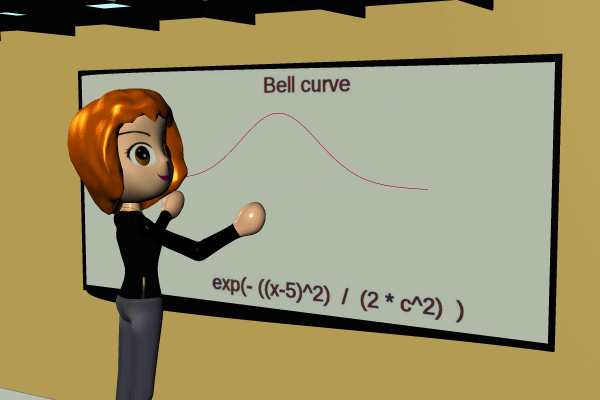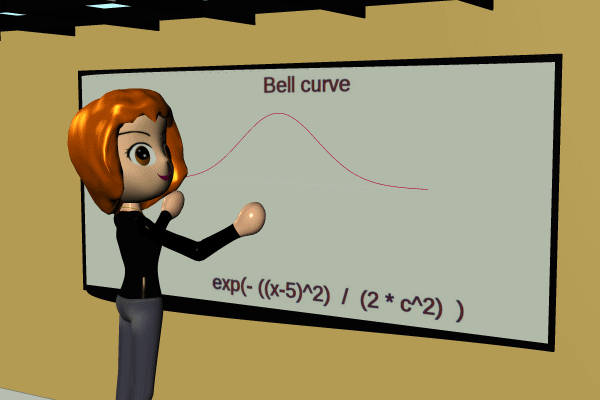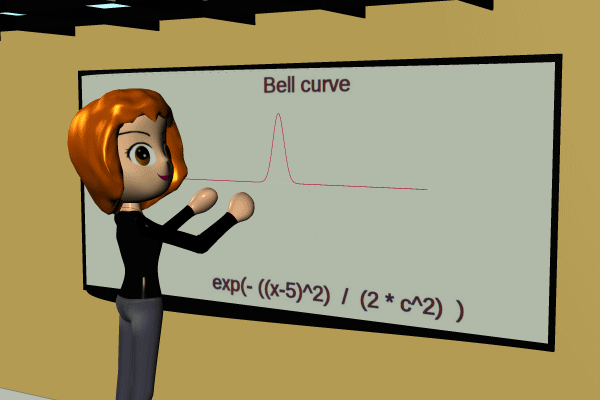 Now the tuning curve:
Now the tuning curve:
 I'm NOT saying that the bell should be replaced by tanh. I'm only showing the distinction dynamically because the tuning curve is unfamiliar. Bell works nicely for stat distributions; one-sided tanh works for most input-output situations (transfer functions) in life, and two-sided tanh it forms the life-patterns of critters and organizations.
The math for the tuning curve is complicated. Computers can handle it, but there should be a nicer way of calculating such a basic and necessary shape. Secular math ought to find a cleaner way of doing it and writing it, whether by an analog calculator or by a single button on a digital calculator.
Another piece of everyday secular math that is NOT handled by sacred math is 'bracketizing', a calculation that uses integers and continua in separate ways, boundaried by decisions, thresholds or containers. I discussed it in the grocery context here and here. Bracketizing also appears in tax forms. When Alleged Einstein called income tax the hardest math problem, he was speaking from a Sacred Math mindset. Calculations like this cannot be turned into a closed-form Sacred equation no matter how hard you try. If line 37 is greater than 3.2 times line 12a, multiply by 0.376; otherwise add 12 and divide by 5.021. A computer program can handle those mixes of decisions and operations, but ideally there should be a way to handle them in 'pure' Secular math.
= = = = =
Question #2: If everything in our life and senses runs logly, why did so much of secular math develop as pure linear addition and subtraction?
Answer: Because one important sense is NOT loggish.
Our senses of pressure and weight are linear. When I put one item, two items, three items, in your hand, the weight-measuring inputs to your brain are linear and even countable. A fast series of pulses from your muscle spindles.
What does that remind you of? Money. One shell, two shells, three shells. One coin, two coins, three coins. Money began as weight, and many monetary units still denote weights.
Because we weighed gold and silver, we became accustomed to treating money, and then transactions involving money, in linear form ... EVEN THOUGH the transactions and our judgments and feelings about the transactions are loggish.
Our sense of relative income is unquestionably log or percentage-based. Even economists have figured this out. As with decibels or lumens, our judgments are the log of the underlying quantity. "My neighbor is one step above me in income" = neighbor has 3 * my income. "If I could jump one step up in wealth I'd be satisfied" = If I had 3 * current wealth I'd be satisfied.
Actual prices of actual goods are also loggish. This is somewhat disguised by the piecewise linearity of a small part of any curve, but when you scale up you can see it. Two cans of soup = same price as one can + one can. Twenty cans of soup cost less than 20 * one can. A thousand cans cost MUCH less than 1000 * one can.
Because overhead is relatively constant, price is a loggish function of quantity.
= = = = =
Question #3: How would commerce and everyday life differ if we had a more loglike system of secular math?
Unanswered for now. As usual, I'm hoping to return to this. As usual, I probably won't.
Later partial answer or starting point.
= = = = =
Bonus:
I've supplied an attempted 'easy proportioner' or 'software slide rule' as mentioned above.
I'm NOT saying that the bell should be replaced by tanh. I'm only showing the distinction dynamically because the tuning curve is unfamiliar. Bell works nicely for stat distributions; one-sided tanh works for most input-output situations (transfer functions) in life, and two-sided tanh it forms the life-patterns of critters and organizations.
The math for the tuning curve is complicated. Computers can handle it, but there should be a nicer way of calculating such a basic and necessary shape. Secular math ought to find a cleaner way of doing it and writing it, whether by an analog calculator or by a single button on a digital calculator.
Another piece of everyday secular math that is NOT handled by sacred math is 'bracketizing', a calculation that uses integers and continua in separate ways, boundaried by decisions, thresholds or containers. I discussed it in the grocery context here and here. Bracketizing also appears in tax forms. When Alleged Einstein called income tax the hardest math problem, he was speaking from a Sacred Math mindset. Calculations like this cannot be turned into a closed-form Sacred equation no matter how hard you try. If line 37 is greater than 3.2 times line 12a, multiply by 0.376; otherwise add 12 and divide by 5.021. A computer program can handle those mixes of decisions and operations, but ideally there should be a way to handle them in 'pure' Secular math.
= = = = =
Question #2: If everything in our life and senses runs logly, why did so much of secular math develop as pure linear addition and subtraction?
Answer: Because one important sense is NOT loggish.
Our senses of pressure and weight are linear. When I put one item, two items, three items, in your hand, the weight-measuring inputs to your brain are linear and even countable. A fast series of pulses from your muscle spindles.
What does that remind you of? Money. One shell, two shells, three shells. One coin, two coins, three coins. Money began as weight, and many monetary units still denote weights.
Because we weighed gold and silver, we became accustomed to treating money, and then transactions involving money, in linear form ... EVEN THOUGH the transactions and our judgments and feelings about the transactions are loggish.
Our sense of relative income is unquestionably log or percentage-based. Even economists have figured this out. As with decibels or lumens, our judgments are the log of the underlying quantity. "My neighbor is one step above me in income" = neighbor has 3 * my income. "If I could jump one step up in wealth I'd be satisfied" = If I had 3 * current wealth I'd be satisfied.
Actual prices of actual goods are also loggish. This is somewhat disguised by the piecewise linearity of a small part of any curve, but when you scale up you can see it. Two cans of soup = same price as one can + one can. Twenty cans of soup cost less than 20 * one can. A thousand cans cost MUCH less than 1000 * one can.
Because overhead is relatively constant, price is a loggish function of quantity.
= = = = =
Question #3: How would commerce and everyday life differ if we had a more loglike system of secular math?
Unanswered for now. As usual, I'm hoping to return to this. As usual, I probably won't.
Later partial answer or starting point.
= = = = =
Bonus:
I've supplied an attempted 'easy proportioner' or 'software slide rule' as mentioned above.
 The proportioner is here. The ZIP contains a (hopefully) self-explanatory Python program. It has an Input side, a Ratio, and an Output side. When you fill in either the numerator or denominator on the Input side, the Ratio shows and the Output side changes appropriately. When you fill in numerator or denominator on the Output side, the Ratio doesn't change, but the other member on the Output side changes.
I've been wanting this little helper for a long time, especially to deal with Aspect Ratio in images. You may find other uses.
The proportioner is here. The ZIP contains a (hopefully) self-explanatory Python program. It has an Input side, a Ratio, and an Output side. When you fill in either the numerator or denominator on the Input side, the Ratio shows and the Output side changes appropriately. When you fill in numerator or denominator on the Output side, the Ratio doesn't change, but the other member on the Output side changes.
I've been wanting this little helper for a long time, especially to deal with Aspect Ratio in images. You may find other uses.Labels: 20th century Dark Age, Experiential education, Real World Math
