Friday, November 06, 2020
COBOL as icon
The Github/Room 101 mindset is the deep terminal disease of recent times. It's a major instance of the psychopathic need to obliterate the universe.
This part of the urge is always present in psychopaths, and it was accurately recognized in earlier times.
Quora's programming language section has some discussions about COBOL that illustrate the distinction beautifully. When I hit Quora just now to find examples, the very first item turned out to be a perfect Self-Explanatory Sentence.....
Digital computers are counters and sorters, not slide rules or theoretical equations on blackboards. Our stupid official history starts with Babbage, who was actually a dead end. Nothing came from Ada except some modern rebuilt legends. The real history of computing starts with Hollerith's counter and sorter, and the real history of programming starts with IBM mainframes counting and sorting money, programmed first in machine codes then soon in COBOL. IBM is uncool, so we can't mention it in our official histories.
Money doesn't use floating point. Money is naturally columnar. I've discussed this in the context of ancient bookkeeping:
= = = = = START REPRINT:
A ledger from the store that was outfitting fur traders in the Louisiana Territory around 1812. It's in French, with some plain English. Deeply fascinating to an old bookkeeper. I'm sure real historians have answered all these questions, but I'm having fun trying to solve them.
Title on first page:
La Compagny des Fourures du Missoury dans son Avanture.
Here's the top few lines of an account for trader Brice Arnold, showing the ledger structure clearly.
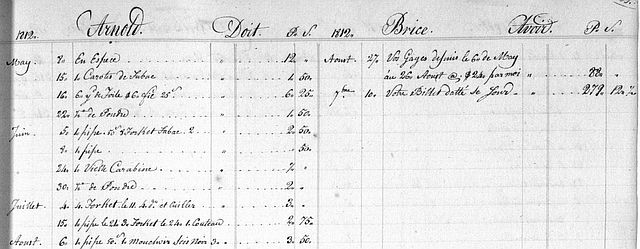The debit column (Doit) is equipment sold to the fur traders, the credit column (Avoir) is furs bought from the traders. Note the Avoir column is closed out with "Your bill given this day."
The money units are puzzling. The two columns are P and S. My first thought was Poids et Shillings, but it appears that Pesos were the dominant currency in the territory at that time.
The S unit is 100ths of the P unit, not 8ths or 20ths. According to online sources, the peso would have been divided into 8 reales at this time, and centavos didn't start until 1863. No firm answer to this question. Was it just US dollars and cents, labeled P and S by tradition?
We have the $ sign on totals, which meant pesos before it meant dollars. One credible explanation of the symbol traces it to a habit of writing an abbreviation for Pesos as a big P with a little s as a diacritic on top. These clerks were precise with their pens, and their dollar sign always had a big belly and a little head. You can almost see a big P with a little s riding on it. They clearly weren't thinking of the whole symbol as an S with lines through it; their uppercase S is entirely different.
Note the marks after each number. Decimal points? Nope, ditto marks. The clerk meticulously repeated the ditto after each number in each column, indicating that all the left numbers were P and all the right numbers were S.
Columnar accounting belongs to the Roman era, not to the modern place-value era. Monetary units were mostly non-decimal, so the tradition of recording each unit in its own independent column made sense, and there was no reason for decimal points. Note that some of the S numbers are followed by fractions, which was still common in US pricing up till WW2 when inflation made fractional cents meaningless.
= = = = = END REPRINT.
Units are not floating point. Fractions are not floating point. Many fractions can't be represented uniquely and cleanly in floating point. A ledger with the proper set of columns corresponding to units can always represent the fractions that people actually use.
The human brain has separate processing systems for analog continua and countable units. We use both in business for different purposes.
The analog side judges the quality and status of different products with the help of senses and muscles. For products that are actually used, like the whiskey and gunpowder and furs in the example, we judge by using and working. We compare one whiskey with another in a totally analog way, leading to an analog decision. You prefer Jack Daniels, but you'll take Old Crow if Jack isn't around. There is no binary step anywhere.
The counting side works with units, which can be single coins or single banknotes or written columns in the ledger.
These units MUST BE DIGITAL. Paying or billing an analog amount is physically impossible and legally meaningless. Decimal currencies hide this fact by eliminating irrational fractions, but through history most currency systems included irrational fractions. In the LSD system, a bill for 5 pence would be 5/12 of 1/20 of a pound, expressed in floating as 0.02083333unending pounds. If we write the bill this way, there's no way to determine whether it was paid properly or not. But if we have a column for pence, we can bill or pay 5 pence and know precisely whether the debt is satisfied.
= = = = =
Later: I installed one of the COBOL compilers for Windows and started learning to use COBOL. This is fun! The more I see how COBOL works, the more I wish I'd tried it in college back in 1967. I'm a natural bookkeeper, not a natural theoretical mathematician. COBOL would have been instantly pleasing to my clerical genes. FORTRAN was always frustrating because I couldn't see the purpose of the examples.
Question: Are there any old programming languages that are still in use? Answer: FORTRAN (63 years), COBOL (60 years), BASIC (56 years), C (48 years), SQL (42 years), C++ (35 years), Objective-C (32 years), Python (29 years), and Java (25 years) are all fairly old and still used (though COBOL is pretty specialized legacy code today). The first three are older than I am.COBOL is specialized legacy code / Older than I am. Self-explanatory sentence. This is the Github view. Old shit is specialized legacy shit and you shouldn't be using it, and we will PROHIBIT YOU FROM USING IT. Any attempt to use tools or thinking from the filthy Neanderthal knuckle-dragging previous femtosecond will halt your life and crash your computer. In the Github world, the PURPOSE of programming is to spend 100% of your mental time relearning, and 100% of your computer's CPU time processing updates. Windows 10 implements this purpose perfectly. What is the original intended purpose of a TOOL like computers? The real purpose of any TOOL is to help you GET WORK DONE. Fortunately the GET WORK DONE side is also well represented in Quora, by older WORKERS and even some younger WORKERS in places like Brazil. Reality: In the world of computers that DO WORK, most of the WORK is done by COBOL. The part of the computing world that is truly needed, the part that would completely collapse the whole economy if it failed, is COBOL. To a first approximation, computing = COBOL. And there's a simple reason, which I didn't understand until I started reading these discussions. I'm older than COBOL but I didn't start programming until 1983, and I didn't start in the world of commerce. I started in audio processing, first with 8086 and PDP-11 assembly, then Basic, then C. Simple reason: COBOL handles money naturally and intrinsically. The newer languages, including FORTRAN, all start from a theoretical math view of numbers where floating-point arithmetic is the base.
Digital computers are counters and sorters, not slide rules or theoretical equations on blackboards. Our stupid official history starts with Babbage, who was actually a dead end. Nothing came from Ada except some modern rebuilt legends. The real history of computing starts with Hollerith's counter and sorter, and the real history of programming starts with IBM mainframes counting and sorting money, programmed first in machine codes then soon in COBOL. IBM is uncool, so we can't mention it in our official histories.
Money doesn't use floating point. Money is naturally columnar. I've discussed this in the context of ancient bookkeeping:
= = = = = START REPRINT:
A ledger from the store that was outfitting fur traders in the Louisiana Territory around 1812. It's in French, with some plain English. Deeply fascinating to an old bookkeeper. I'm sure real historians have answered all these questions, but I'm having fun trying to solve them.
Title on first page:
La Compagny des Fourures du Missoury dans son Avanture.
Here's the top few lines of an account for trader Brice Arnold, showing the ledger structure clearly.
The debit column (Doit) is equipment sold to the fur traders, the credit column (Avoir) is furs bought from the traders. Note the Avoir column is closed out with "Your bill given this day."
The money units are puzzling. The two columns are P and S. My first thought was Poids et Shillings, but it appears that Pesos were the dominant currency in the territory at that time.
The S unit is 100ths of the P unit, not 8ths or 20ths. According to online sources, the peso would have been divided into 8 reales at this time, and centavos didn't start until 1863. No firm answer to this question. Was it just US dollars and cents, labeled P and S by tradition?
We have the $ sign on totals, which meant pesos before it meant dollars. One credible explanation of the symbol traces it to a habit of writing an abbreviation for Pesos as a big P with a little s as a diacritic on top. These clerks were precise with their pens, and their dollar sign always had a big belly and a little head. You can almost see a big P with a little s riding on it. They clearly weren't thinking of the whole symbol as an S with lines through it; their uppercase S is entirely different.
Note the marks after each number. Decimal points? Nope, ditto marks. The clerk meticulously repeated the ditto after each number in each column, indicating that all the left numbers were P and all the right numbers were S.
Columnar accounting belongs to the Roman era, not to the modern place-value era. Monetary units were mostly non-decimal, so the tradition of recording each unit in its own independent column made sense, and there was no reason for decimal points. Note that some of the S numbers are followed by fractions, which was still common in US pricing up till WW2 when inflation made fractional cents meaningless.
= = = = = END REPRINT.
Units are not floating point. Fractions are not floating point. Many fractions can't be represented uniquely and cleanly in floating point. A ledger with the proper set of columns corresponding to units can always represent the fractions that people actually use.
The human brain has separate processing systems for analog continua and countable units. We use both in business for different purposes.
The analog side judges the quality and status of different products with the help of senses and muscles. For products that are actually used, like the whiskey and gunpowder and furs in the example, we judge by using and working. We compare one whiskey with another in a totally analog way, leading to an analog decision. You prefer Jack Daniels, but you'll take Old Crow if Jack isn't around. There is no binary step anywhere.
The counting side works with units, which can be single coins or single banknotes or written columns in the ledger.
These units MUST BE DIGITAL. Paying or billing an analog amount is physically impossible and legally meaningless. Decimal currencies hide this fact by eliminating irrational fractions, but through history most currency systems included irrational fractions. In the LSD system, a bill for 5 pence would be 5/12 of 1/20 of a pound, expressed in floating as 0.02083333unending pounds. If we write the bill this way, there's no way to determine whether it was paid properly or not. But if we have a column for pence, we can bill or pay 5 pence and know precisely whether the debt is satisfied.
= = = = =
Later: I installed one of the COBOL compilers for Windows and started learning to use COBOL. This is fun! The more I see how COBOL works, the more I wish I'd tried it in college back in 1967. I'm a natural bookkeeper, not a natural theoretical mathematician. COBOL would have been instantly pleasing to my clerical genes. FORTRAN was always frustrating because I couldn't see the purpose of the examples.Labels: defensible cases, defensible thymes, defensible times, Real World Math, SES
¶ 11:28 PM
