Tuesday, March 11, 2014
Steppy and saggy
Continuing the theme of step functions, cliffs, slopes..... Back in September Polistra noted that the seasons were running in an especially steppy way. The steppiness has continued with the winter-to-spring transition. We had a short burst of single digits at the end of a long solid cold spell, then SNAP! All the way up to 60 degrees with lots of rain.
This is an extreme case of a fairly typical pattern here. In electronics the Spokane seasons would reduce to an 'underdamped' response, like this.....
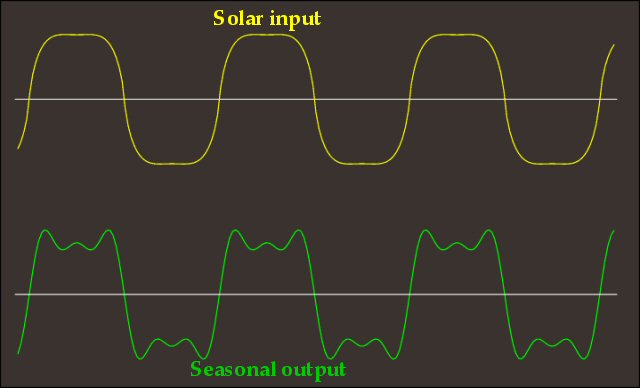 The sun's input across the seasons (yellow line above) is a soft-saturated or flattop sine. The seasonal response (green line) is underdamped, with overshoot on the spring/fall deltas and a sag toward the mean in summer and winter.
= = = = =
Playing with black boxes..... If we assume that the local climate involves some kind of negative feedback, we can characterize the feedback.
= = = = =
First, could it be a strictly linear feedback, with no storage or filtering? In that case it would behave like the first animation. Mr Sun gives his flattop input to the Op-Amp. Feedback is nothing but a voltage divider, as visualized by the bouncing ball. Strictly following Mr Sun. Result, unsurprisingly, is the same flattop sine. This won't do.
The sun's input across the seasons (yellow line above) is a soft-saturated or flattop sine. The seasonal response (green line) is underdamped, with overshoot on the spring/fall deltas and a sag toward the mean in summer and winter.
= = = = =
Playing with black boxes..... If we assume that the local climate involves some kind of negative feedback, we can characterize the feedback.
= = = = =
First, could it be a strictly linear feedback, with no storage or filtering? In that case it would behave like the first animation. Mr Sun gives his flattop input to the Op-Amp. Feedback is nothing but a voltage divider, as visualized by the bouncing ball. Strictly following Mr Sun. Result, unsurprisingly, is the same flattop sine. This won't do.
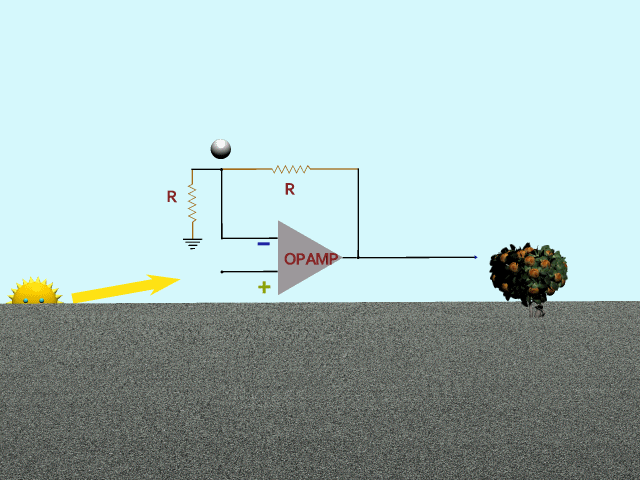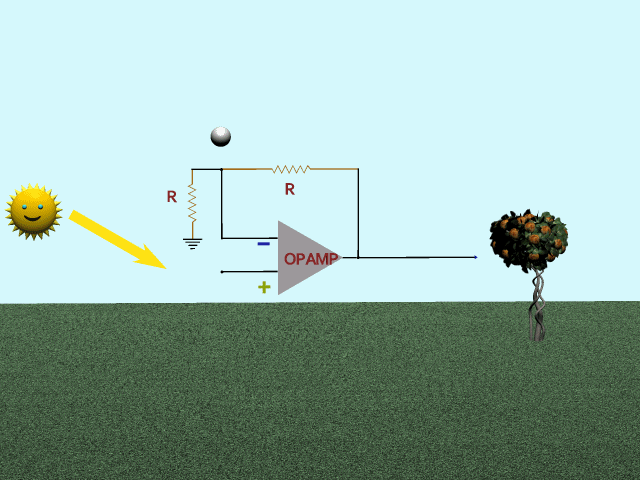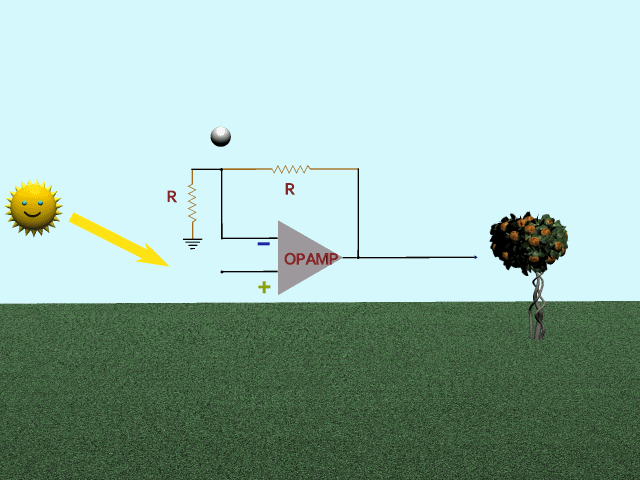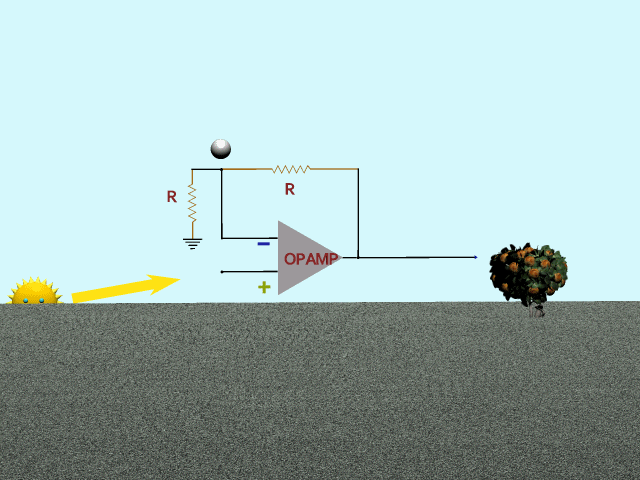 = = = = =
Second, could the feedback be a high-pass filter? In that case it would behave like this second animation. Mr Sun gives the identical flattop input. Feedback (bouncing ball) is high-passed, giving only the deltas to the inverting input. Result would be a retardation of the ups and downs in spring and fall, and an emphasis on winter and summer. Nope, that's not it either.
= = = = =
Second, could the feedback be a high-pass filter? In that case it would behave like this second animation. Mr Sun gives the identical flattop input. Feedback (bouncing ball) is high-passed, giving only the deltas to the inverting input. Result would be a retardation of the ups and downs in spring and fall, and an emphasis on winter and summer. Nope, that's not it either.
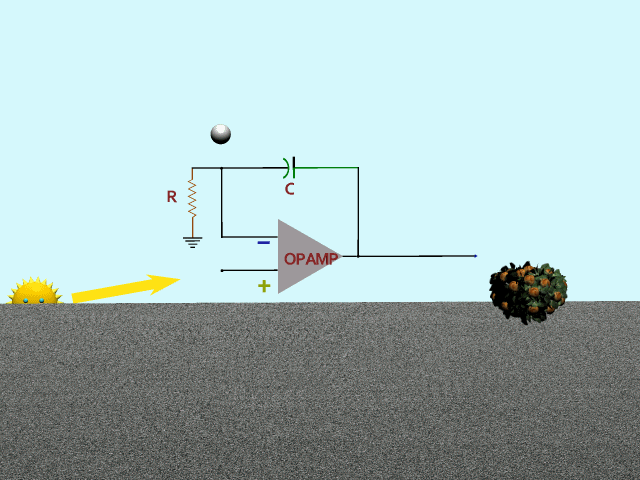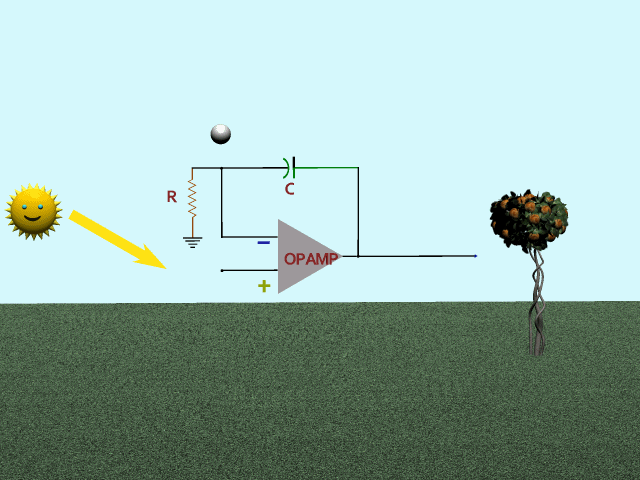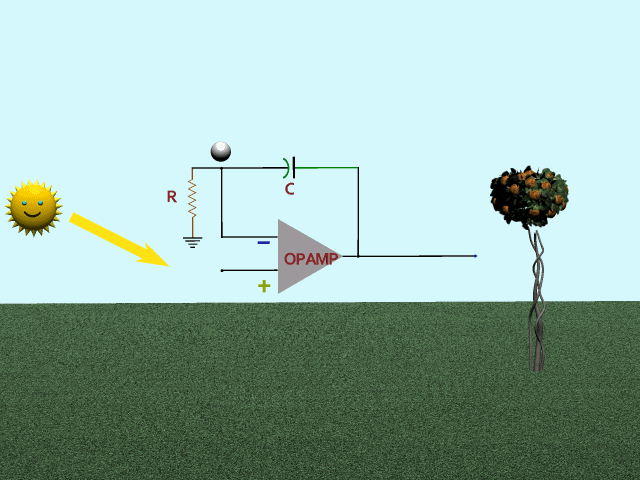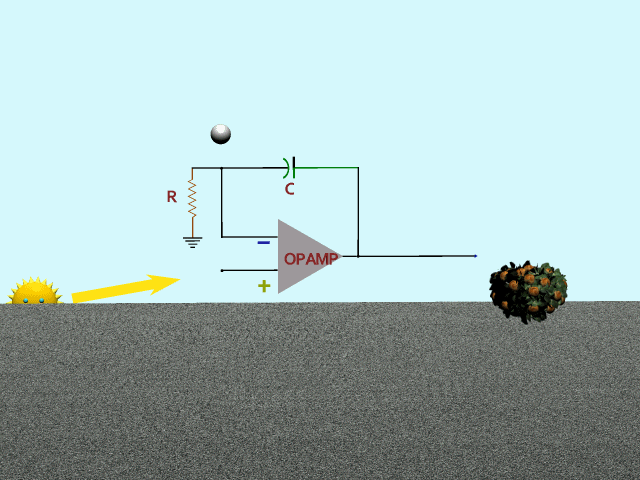 = = = = =
Third, how about a low-pass filter for feedback? Mr Sun does his thing again. Feedback (bouncing ball) responds slowly to spring and fall, gradually reaching full top and bottom values. Result is an emphasis on the ups and downs in spring and fall, and a sag during the flattop times.
= = = = =
Third, how about a low-pass filter for feedback? Mr Sun does his thing again. Feedback (bouncing ball) responds slowly to spring and fall, gradually reaching full top and bottom values. Result is an emphasis on the ups and downs in spring and fall, and a sag during the flattop times.
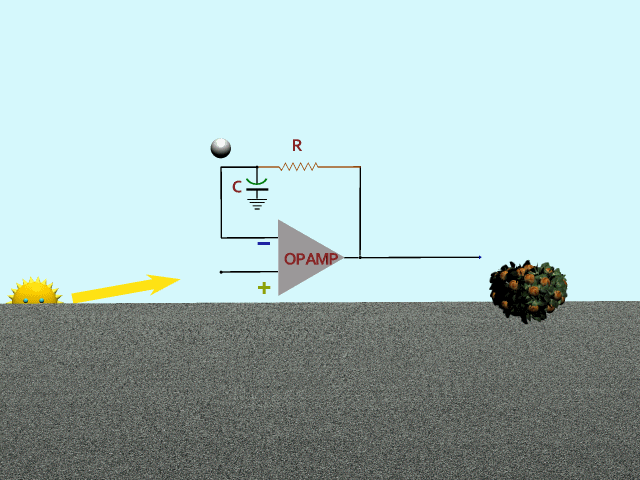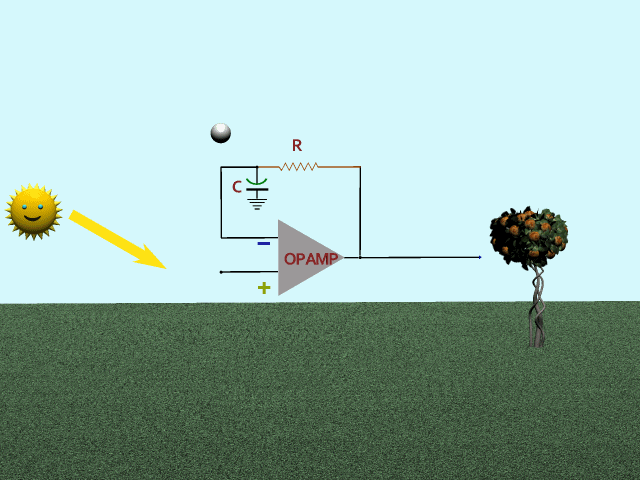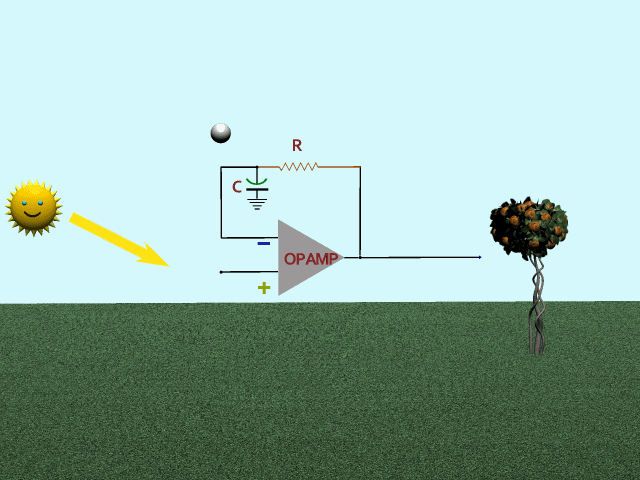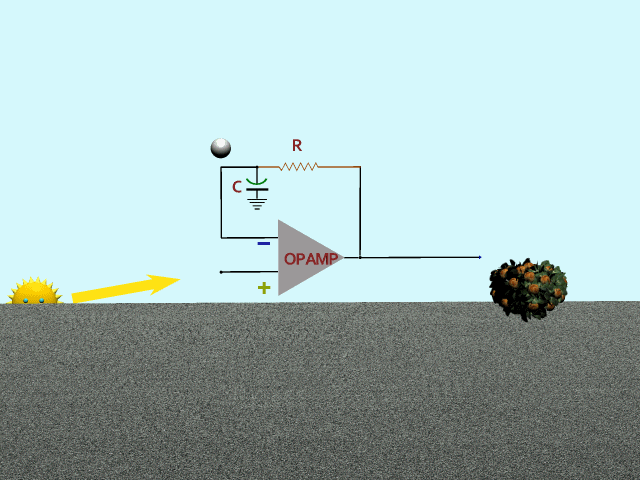 That's it! Goldilocks!
That's it! Goldilocks!
 The sun's input across the seasons (yellow line above) is a soft-saturated or flattop sine. The seasonal response (green line) is underdamped, with overshoot on the spring/fall deltas and a sag toward the mean in summer and winter.
= = = = =
Playing with black boxes..... If we assume that the local climate involves some kind of negative feedback, we can characterize the feedback.
= = = = =
First, could it be a strictly linear feedback, with no storage or filtering? In that case it would behave like the first animation. Mr Sun gives his flattop input to the Op-Amp. Feedback is nothing but a voltage divider, as visualized by the bouncing ball. Strictly following Mr Sun. Result, unsurprisingly, is the same flattop sine. This won't do.
The sun's input across the seasons (yellow line above) is a soft-saturated or flattop sine. The seasonal response (green line) is underdamped, with overshoot on the spring/fall deltas and a sag toward the mean in summer and winter.
= = = = =
Playing with black boxes..... If we assume that the local climate involves some kind of negative feedback, we can characterize the feedback.
= = = = =
First, could it be a strictly linear feedback, with no storage or filtering? In that case it would behave like the first animation. Mr Sun gives his flattop input to the Op-Amp. Feedback is nothing but a voltage divider, as visualized by the bouncing ball. Strictly following Mr Sun. Result, unsurprisingly, is the same flattop sine. This won't do.
 = = = = =
Second, could the feedback be a high-pass filter? In that case it would behave like this second animation. Mr Sun gives the identical flattop input. Feedback (bouncing ball) is high-passed, giving only the deltas to the inverting input. Result would be a retardation of the ups and downs in spring and fall, and an emphasis on winter and summer. Nope, that's not it either.
= = = = =
Second, could the feedback be a high-pass filter? In that case it would behave like this second animation. Mr Sun gives the identical flattop input. Feedback (bouncing ball) is high-passed, giving only the deltas to the inverting input. Result would be a retardation of the ups and downs in spring and fall, and an emphasis on winter and summer. Nope, that's not it either.
 = = = = =
Third, how about a low-pass filter for feedback? Mr Sun does his thing again. Feedback (bouncing ball) responds slowly to spring and fall, gradually reaching full top and bottom values. Result is an emphasis on the ups and downs in spring and fall, and a sag during the flattop times.
= = = = =
Third, how about a low-pass filter for feedback? Mr Sun does his thing again. Feedback (bouncing ball) responds slowly to spring and fall, gradually reaching full top and bottom values. Result is an emphasis on the ups and downs in spring and fall, and a sag during the flattop times.
 That's it! Goldilocks!
That's it! Goldilocks!
