Average temperature again
Polistra has logically debunked the notion that you can have an "average temperature" for the globe. Partial reprint:

= = = = =

Averaging temperatures at two locations to make a single temperature is a really basic statistical error that I learned about in junior high science class.

Remember this? The teacher turns on a cold faucet and a hot faucet; puts her right hand under the cold faucet and her left hand under the hot. Says "My right hand is at 40 degrees and my left hand is at 110 degrees. Therefore my average hand is at 75 degrees, which is Just Right!"



The more alert students get the point immediately and laugh.

= = = = =END REPRINT

You can use math to form 'predictors' (averages, models, extrapolations) only when the measurements are part of a continuum. Averaging two water temps could make sense if the waters were actually being mixed, which creates a continuum.



Here I measured the temperature of water drawn from my cold faucet and hot faucet separately, then filled the glass with half cold and half hot. Valid use of the mean, because the water molecules of two different energies are interspersed, subject to the same influences, which allows you to figure a net energy for the mixture.

Mean(95,62)=78.5, and actual mix is about 78. Pretty close.

[Artistic note: I wasn't trying to create a red atmosphere for the warm temps; the digital camera did that on its own. Clearly I don't know how to use it yet!!!!]

= = = = =

The mean of two locations can be valid when the two places are nearby and definitely subject to all the same influences at the same time. In that case you know there's a continuous range between them, so that interpolation is meaningful.



In this scenario, Happystar is nicely ensconced in the warm interior of the house, say 70 degrees. Garbanzo is outside in 50 degrees. Polistra (aka Goldilocks) is on the screened back porch, slightly sheltered from outside, with some radiant input from the house. Probably somewhere around 57 degrees. If she walked through the door into the house, she would experience a gradual increase from 57 to 70. Smooth interpolation, so a weighted mean or calibration curve would be useful for prediction.

By contrast, here's a real-world situation where interpolation fails completely. I captured the Wunderground interactive map of the Spokane area this morning, then circled 5 places where interpolation fails.



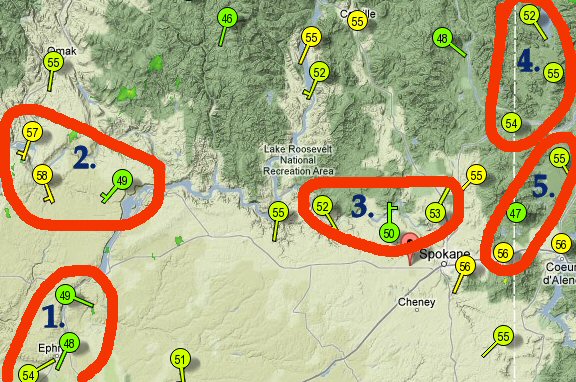In each case the real in-between temperature is either less than both of the extremes or greater than both of the extremes.

[1] Mean(54,49)=51.5 but actual is less than 49.

[2] Mean(57,49)=53.0 but actual is greater than 57.

[3] Mean(53,52)=52.5 but actual is less than 52.

[4] Mean(54,52)=53.0 but actual is greater than 54.

[5] Mean(56,55)=55.5 but actual is less than 55.

Any attempt to form a spatial average across these non-continuous values will be utterly meaningless and futile. These temps are independent just like the two faucets in the first example. There is no linear function relating them, so you can't try to find the midpoint of that (nonexistent) linear function.

Averaging already fails in these 30-mile circles, so it's even worse when you try to mix the separate atmospheric systems of the northern and southern hemispheres to make a "global" average.

Labels: Blinded by Stats, Carbon Cult

  ¶ 5:10 AM