How abstract is negative?
Further to this discussion of abstraction in our number sense. None, some, zero, three, etc.

Repeating the main point: It's easy to see why zero was a late development. Without any mental strain we can say things like "None of the cars are in my yard." This is not a zero concept. We know what cars are, and we know that cars are present somewhere, or were in the yard earlier. Cars are simply not in the yard here and now. We have more strain with a true zero, like "none of the things are in my yard." How can you possibly have a yard with Zero Things?

Extending this line of thought, we run into an oddity. Negative numbers were invented by those ancient Hindoos along with zero, but negatives haven't penetrated ordinary thought and discourse. In modern times zero is part of basic literacy, If you can read, you know how to use zero. Not so with negatives. We don't use negatives unless we have learned "higher" math, and we don't use them unless we do math for "higher" professional purposes. Negatives don't appear in newspaper articles or maps or price lists or advertisements. With one partial exception, nobody ever speaks a negative number on TV or radio. (Negative temperature is usually spoken as "five degrees below zero", rarely "negative five degrees.")

Here's the oddity: Zero is not natural, but negatives are natural. Most of our senses are bidirectional, with two directional deltas from an arbitrary neutral or center point. Cold<--->Hot, Big<--->Small, Light<--->Dark, Good<--->Bad, Smart<--->Dumb, Rich<--->Poor, High<--->Low.

Some of these axes correspond to unidirectional physical measurements that have a zero at one end, but our sensory neutral point is rarely at the physical zero point. In most cases the neutral point is mobile, simply adapted to the status quo.

In our minds and feelings, the two end vectors are distinct places with distinct personalities. The midpoint also has a distinct personality, usually connoting something like 'mainstream' or 'normal' or 'undistinguished'.

= = = = =

City maps show this tendency in a Cartesian way.

American cities fall into six major types. The first two are the far ends of the spectrum, not especially interesting for my purpose here.

(1) Ancient Euro-style places like Boston and Santa Fe. Streets may be one block long, or might wander aimlessly for a mile or two. All streets are named. No numbers at all, no perpendicularity at all.

(2) Nearly pure numerical grids like Seattle and Salt Lake. Except for some major boulevards or landmarks, all streets are numbered, with a complex set of prefixes and suffixes. Avenue 120 Southwest and 34th North Street and 247th EastNorth Way and South Place 532 East and so on.

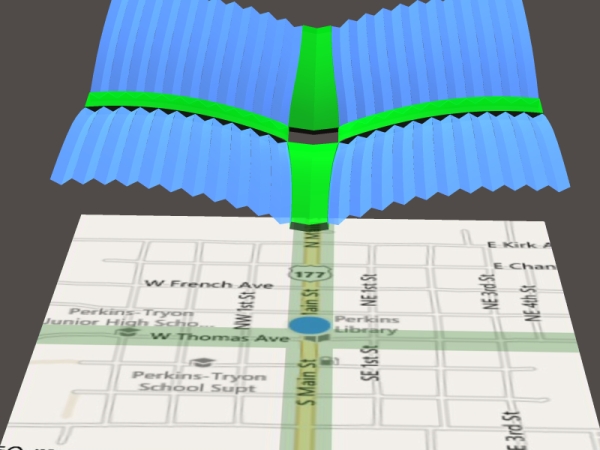
(3) The symmetrical names vs numbers cross. Typified by OKC, copied by many smaller towns in Okla and vicinity. As shown here on little Perkins, all vertical streets are numbered, running both ways from the X-axis of Thomas. All horizontal streets are named, running both ways from the Y axis of Main. The whole thing could be turned 90 degrees, but I'll stick with one description for clarity. In math terms, this is four equivalent quadrants. The bizarre accordiony thing upstairs is my attempt to show how the numbering pattern 'feels'.



(4) The asymmetrical names vs numbers cross. I think this is the most common pattern in the Midwest. Shown here on a map of Enid. All horizontal streets are named, and have East and West directions from the Y-axis of Grand. Vertical streets east of Grand are numbered. Vertical streets west of Grand are named, with a memorable sequence of presidents instead of numbers. In math terms, you could call this a four-quadrant grid with the Y-axis separating different flavors. Again the pattern could be turned 90 degrees.



(5) The names vs numbers T-shape. This sometimes happens when a river provides a natural and effectively uncrossable zero point. Manhattan shows it nicely. All horizontal streets are named, with no West or East. They all go West from the Y-axis of the river, so 'negative' isn't needed. All vertical streets are numbered, with North and South starting from the X-axis of Poyntz. This is a two-quadrant graph.



(6) I suppose there must be some one-quadrant cities with no mirror-images at all, but I've never seen one. Some nominally four-quad cities failed to develop in two directions and ended up close to this situation, but they retain the pretense of having NSEW sections. It's hard to tell from modern online maps because lots of tiny towns have lost their original street names. The Post Office generally 'rationalizes' those towns with robotic county-based coordinates like ROAD 13840. Probably doesn't matter to local residents. Before 'rationalization' they didn't know that Charlie's house was at NE 2nd and E. Walnut. Now they don't know that Charlie's house is 54182 ROAD 13840. It's still just Charlie's house.

= = = = =

The dominance of bidirectionality, with streets running both ways from the Main Street midpoint, corresponds nicely to our sensory bidirectionality. We want to have a midpoint as 'home base', and we want to go ... or at least imagine that we can go ... either way from the 'home base'. We also want the two sides to have different flavors and different anticipations, not just a single symbol like + vs - or N vs S. Upstream, downstream, left bank, right bank.

Most cities have a single rule for odd vs even numbers. South side of horizontal streets is even, east side of vertical streets is even. (Or vice versa on each; but it's the same through the whole city.) Spokane's odd-even pattern seems inconsistent if you're just looking at a map. Each quadrant seems to have its own rule. But the pattern makes perfect sense from the upstream-downstream viewpoint. Single rule: If you're going upstream, away from centerline, you'll see even houses on your right. For example: When you're east of Division and heading east, you're going upstream, so even is on your right. When you're north of Sprague and heading north, you're going upstream, so even is on your right.

Labels: Metrology

  ¶ 5:32 AM